Study of an IWRR tandem

info

The examples shown in this page can be found, in notebook form, on GitHub.

Using the IWRR model in the previous page, we can exemplify a study where non-convex service curves arise, hence a case where the flexibility of Nancy is useful.

Consider a flow traversing a tandem network of 2 server nodes. Access to each node is independently regulated using IWRR scheduling (with a different set of cross flows).

We consider the flow to be shaped by a token-bucket arrival curve. At each node, the flow is given an allocation matching said rate. For the DNC analysis, we use again the IWRR model described in [TLBB21].

First we (trivially) generalize the IWRR service curve computation as IwrrServiceCurve().

Curve IwrrServiceCurve(int foi, int[] weights, int[] l_min, int[] l_max, SuperAdditiveCurve beta)
{
    var unit_rate = new RateLatencyServiceCurve(1, 0);

    // parameters computation omitted for brevity
    int Phi_i_j(int i, int j, int x) { ... }
    int Psi_i(int i, int x) { ... }
    int L_tot(int i) { ... }
    
    var stairs = new List<Curve>();
    for(int k = 0; k < weights[foi]; k++)
    {
        var stair = new StairCurve(l_min[foi], L_tot(foi));
        var delayed_stair = stair.DelayBy(Psi_i(foi, k * l_min[foi])); 
        stairs.Add( delayed_stair );
    }
    var U_i = Curve.Addition(stairs); // summation of min-plus curves
    var gamma_i = Curve.Convolution(unit_rate, U_i);
    var beta_i = Curve.Composition(gamma_i, beta);
    return beta_i;
}

Then, we define the parameters of our network

// ms as time unit, bit as data unit
// the flow has a max arrival rate of 10 Mbps, and is guaranteed such bandwidth at each node
var foi_ac = new SigmaRhoArrivalCurve(1024, 10000);

// 100 Mb/s, 1 ms of latency
// 3 cross flows
var b1 = new RateLatencyServiceCurve(100000, 1);
var weights_1 = new []{10, 30, 40, 20};
var l_min_1 = new []{512, 512, 512, 512};
var l_max_1 = new []{1024, 1024, 1024, 1024};

// 200 Mb/s, 1 ms of latency
// 5 cross flows
var b2 = new RateLatencyServiceCurve(200000, 1);
var weights_2 = new []{10, 20, 40, 50, 30, 50};
var l_min_2 = new []{512, 512, 512, 512, 512, 512};
var l_max_2 = new []{1024, 1024, 1024, 1024, 1024, 1024};

We can now compute the IWRR service curve at each node.

var b_eq_1 = IwrrServiceCurve(0, weights_1, l_min_1, l_max_1, b1);
var b_eq_2 = IwrrServiceCurve(0, weights_2, l_min_2, l_max_2, b2);

Figure 1: Plot of the IWRR service curves at the two nodes.

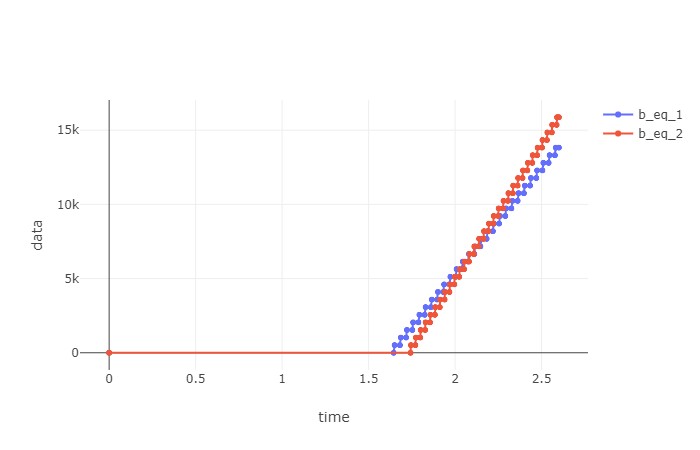
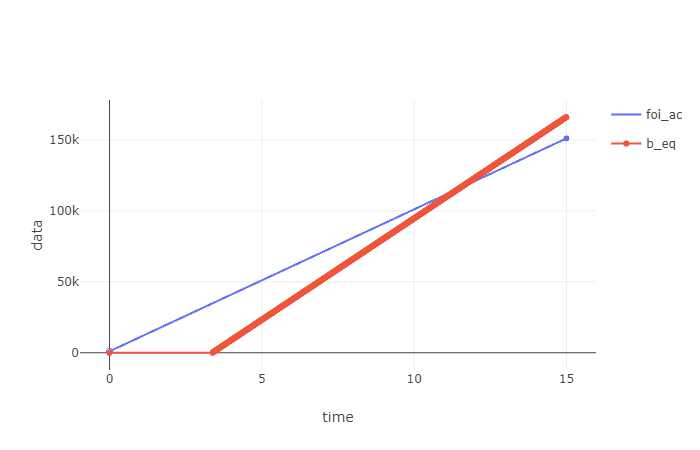
Note that the above are non-convex, and their period lengths are not integers. We complete the study by computing the equivalent service curve for the tandem using the min-plus convolution, and then computing the worst-case delay and backlog bounds as, respectively, the horizontal and the vertical deviation between the foi arrival curve and said service curve.

var b_eq = Curve.Convolution(b_eq_1, b_eq_2);
var delay_bound = Curve.HorizontalDeviation(foi_ac, b_eq);
// Output: 3,46 ms
var backlog_bound = Curve.VerticalDeviation(foi_ac, b_eq);
// Output: 34900 bit

Figure 2: Plot of the equivalent service curve and the foi arrival curve.