Main types

UPP functions

To understand the types, we first explain what we are trying to represent: Ultimately Pseudo-Periodic piecewise affine (henceforth, UPP) functions [Dnc18], meaning that

$$f(t + k \cdot d) = f(t) + k \cdot c , \forall~t \ge T, k \in \mathbb{N}$$

Ok, let's unpack this.

Ultimately means that this property applies for $t \ge T$, rather than all $t$. Pseudo-Periodic means that the function repeats with the same behavior after a period $d$, but with a static gain $c$ that is accumulated at each repetition. Piecewise affine means that the graph of the function is a series of points and segments.

We focus on these functions because they can be fully described with a finite representation, thus a finite data structure. For example, for the curve below we only need to store the points and segments in $[0, 4[$: the point and segments in $[2, 4[$ are repeated indefinetely ($d = 2$, $c = 4$) thus the rest can be derived on-demand.

Figure 1: Example of UPP curve.

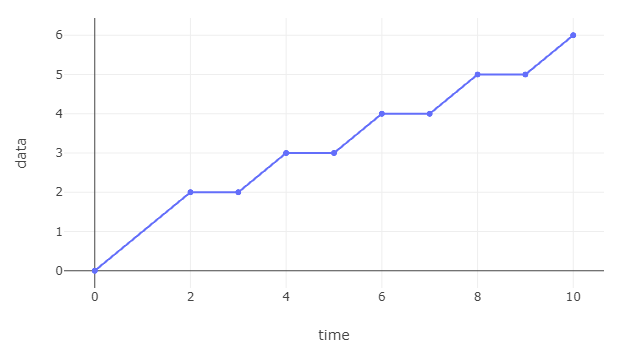
The types

Nancy's main types are:

• Point, a single time-value pair, and Segment, defined in open interval $]a, b[$
• Sequence, which is piecewise affine function defined in a limited interval (can be opened, closed, a mix of both), constructed as a series of Points and Segments.
• Curve, which is the representation of a UPP function, constructed as a Sequence defined in $[0, T + d[$ and the three parameters PseudoPeriodStart $(T)$, PseudoPeriodLength $(d)$ and PseudoPeriodHeight $(c)$.

For example, here is the code for the curve in Figure 1:

var c = new Curve(
    baseSequence: new Sequence(new Element[]
    {
        new Point(time: 0, value: 0),
        new Segment(startTime: 0, endTime: 2, rightLimitAtStartTime: 0, slope: 1),
        new Point(2, 2),
        new Segment(2, 3, 2, 0),
        new Point(3, 2),
        new Segment(3, 4, 2, 1)
    }),
    pseudoPeriodStart: 2,   // T
    pseudoPeriodLength: 2,  // d
    pseudoPeriodHeight: 1   // c
);

References

• [1] Deterministic Network Calculus: From Theory to Practical Implementation, A. Bouillard and M. Boyer and E. Le Corronc, 2018