Passa al contenuto principale

Esercitazione 4

In questa esercitazione vedremo un esercizio d'esame svolto interamente, sia come descrizione che come sintesi. Il testo dell'esercizio è scaricabile qui.

Esercizio 4.1: Descrizione​

La rete sincronizzata ABC deve ottenere tre valori da altrettanti produttori, sostenendo tre handshake soc/eoc indipendenti. Tipicamente, questo vuol dire che siamo liberi di eseguire i tre handshake in qualunque ordine, per esempio in serie. In questo caso però, avendo una sola uscita soc, siamo costretti a far proseguire i tre handshake secondo gli stessi passi.

Se deriviamo il seguente algoritmo per ABC:

  • A riposo: soc a 0, tutti gli eoc a 1, i dati sono validi
  • Inizia ABC mettendo soc a 1
  • Attende la risposta eoc a 0 da tutti i produttori
  • Risponde con soc a 0
  • Attende la conferma eoc a 1 da tutti i produttori
  • A questo punto, i dati sono validi, e lo resteranno fino al prossimo ciclo

Alla fine di un tale handshake, possiamo svolgere il conto. Le specifiche fanno riferimento a trovare il minimo tra le tensioni v1v_1, v2v_2 e v3v_3, che sono, in generale, numeri reali, non rappresentabili in un numero finito di bit.

Tramite i convertitori da analogico a digitale si utilizza però una legge di corrispondenza che associa, con un certo errore, a ogni valore reale vv un il valore xx rappresentabile su un numero finito di bit. In questo caso, l'esercizio specifica che queste tensioni sono rappresentate in binario unipolare: questo significa che i vari xx sono numeri naturali. Questa associazione preserva gli ordinamenti: a x1≤x2x_1 \le x_2 corrisponde v1≤v2v_1 \le v_2. Possiamo quindi tradurre il problema di minimo tra tensioni vv in un problema di minimo tra naturali xx.

Il risultato dovrà poi essere trasferito al consumatore usando un handshake dav_/rfd. Per far questo, deriviamo il seguente algoritmo per ABC:

  • A riposo: dav_ a 1, rfd a 1
  • All'ottenimento di un nuovo dato da trasferire, si imposta l'uscita min a tale dato e solo poi si mette dav_ a 0 per segnalarlo. L'uscita min non può oscillare o cambiare
  • Si attende la risposta rfd a 0
  • Si mette dav_ a 1, ora l'uscita min è di nuovo libera di oscillare o cambiare
  • Si aspetta la risposta con rfd a 1

Possiamo quindi scrivere la seguente descrizione in Verilog, scaricabile qui.

module ABC(
    x1, x2, x3,
    eoc1, eoc2, eoc3,
    soc,
    min, dav_, rfd,
    clock, reset_
);
    input [7:0] x1, x2, x3;
    input eoc1, eoc2, eoc3;
    output soc;
    output [7:0]min;
    output dav_;
    input rfd;
    input clock, reset_;

    reg SOC;
    assign soc = SOC;
    reg [7:0] MIN;
    assign min = MIN;
    reg DAV_;
    assign dav_ = DAV_;

    reg [1:0] STAR;
    localparam 
        S0 = 0,
        S1 = 1,
        S2 = 2,
        S3 = 3;

    wire [7:0] out_rc;
    MINIMO_3 min_rc(
        .a(x1), .b(x2), .c(x3),
        .min(out_rc)
    );

    always @(reset_ == 0) #1 begin
        SOC <= 0;
        DAV_ <= 1;
        STAR <= 0;
    end

    always @(posedge clock) if(reset_ == 1) #3 begin
        casex (STAR)
            S0: begin
                SOC <= 1;
                STAR <= ({eoc1, eoc2, eoc3} == 3'b000) ? S1 : S0;
            end

            S1: begin
                SOC <= 0;
                MIN <= out_rc;
                STAR <= ({eoc1, eoc2, eoc3} == 3'b111) ? S2 : S1;
            end

            S2: begin
                DAV_ <= 0;
                STAR <= (rfd == 1) ? S2 : S3;
            end

            S3: begin
                DAV_ <= 1;
                STAR <= (rfd == 0) ? S3 : S0;
            end

        endcase
    end

endmodule

module MINIMO_3(
    a, b, c,
    min
);
    input [7:0] a, b, c;
    output [7:0] min;

    assign #2 min = (a >= b) ? ((b >= c) ? c : b )
                             : ((a >= c) ? c : a );

endmodule
La descrizione della rete combinatoria è opzionale

Gli esercizi d'esame chiedono descrizione e sintesi per la rete sincronizzata, ma solo la sintesi per la rete combinatoria. È quindi del tutto opzionale mostrare una descrizione di quest'ultima.

È spesso però utile scrivere prima una descrizione, soprattutto se facilmente interpretabile. Così facendo, in caso di errori nei test, sappiamo di dover debuggare solo la descrizione della rete sincronizzata.

Esercizio 4.1: Sintesi della rete combinatoria​

La rete da sintetizzare calcola il minimo di tre numeri naturali. Cominciamo osservando che il minimo di tre numeri è un problema che si può scomporre per associatività: min⁡(a,b,c)=min⁡(min⁡(a,b),c)\min(a, b, c) = \min( \min(a, b), c ). Questo vuol dire che posso costruire una reti combinatoria per il minimo di tre numeri combinando solo reti per il minimo di due numeri. Lo stesso principio si generalizza per il minimo di nn numeri.

Nell'esercizio 2.1 abbiamo visto come costruire una rete combinatoria per il massimo tra due numeri, utilizzando un comparatore. Modificare tale rete per produrre il minimo anziché il massimo è semplice, basta cambiare il multiplexer in fondo. Dato che questo esercizio ci fornisce un sottrattore, possiamo usarlo direttamente anziché costruirlo come nell'esercizio 2.1

module MINIMO_2(
    a, b,
    min
);
    input [7:0] a, b;
    output [7:0] min;

    wire b_out;
    diff #( .N(8) ) d(
        .x(a), .y(b), .b_in(1'b0),
        .b_out(b_out)
    );

    assign #1 min = b_out ? a : b;
endmodule

Essendo questa una sintesi di MINIMO_2, possiamo usare questo componente per la sintesi di MINIMO_3.

module MINIMO_3(
    a, b, c,
    min
);
    input [7:0] a, b, c;
    output [7:0] min;

    // min_3(a, b, c) = min_2( min_2(a, b), c );

    wire [7:0] m_ab_out;
    MINIMO_2 m_ab(
        .a(a), .b(b),
        .min(m_ab_out)
    );

    MINIMO_2 m_abc(
        .a(m_ab_out), .b(c),
        .min(min)
    );
endmodule

Esercizio 4.1: Sintesi di rete sincronizzata​

La descrizione di una rete sincronizzata è molto utile a capire come si evolve nel tempo: mette in evidenza lo stato interno (registro STAR), i suoi registri operativi, e come questi cambiano nel tempo in base sia al loro contenuto sia agli ingressi della rete.

Quest'uso del Verilog è affine a un diagramma di stato della stessa rete: è certamente più prolisso (per rendere il codice non ambiguo e simulabile) ma è comunque facile seguire l'evoluzione della rete usando una descrizione Verilog allo stesso modo in cui si fa lo stesso con un diagramma di stato.

Una sintesi, invece, si occupa di dirci come realizzare tale rete. In teoria, per le descrizioni che scriviamo servirebbero solitamente pochi accorgimenti perché siano direttamente realizzabili in hardware. In pratica, però, questo porterebbe a un uso particolarmente costoso e inefficiente di silicio. Seguiamo quindi un algoritmo euristico che ci porta ad hardware molto più efficiente, ragionevolmente vicino a qualcosa che ha senso realizzare.

Non esiste l'ottimo

I ragionamenti fatti in questo corso sull'ottimalità delle sintesi portano solo laddove ci può portare la matematica. Per andare oltre, bisogna entrare nei dettagli pratici, e affrontare trade-off tra processi di produzione, costi in termini di superfice, consumi energetici, esposizione a rischi di progettazione, etc. La progettazione di circuiti integrati è un tema di ingegneria a sé.

Corrispondenza tra sintesi e descrizione

Una sintesi corrisponde a una descrizione: mostra più in dettaglio come realizzare in hardware una rete che si comporta, esternamente, allo stesso modo della descrizione. Una sintesi che si comporti in modo diverso dalla descrizione non ha alcun senso.

Il modello di sintesi che ci aspettiamo negli esercizi d'esame è il modello con parte operativa e parte controllo, dove la parte controllo è implementata secondo il modello a microindirizzi.

Riassumendo, questo significa che:

  • la rete è divisa in una parte operativa, che contiene solo i registri operativi e le relative reti combinatorie, e una parte controllo, che contiene il solo registro di stato STAR
  • La parte operativa riceve variabili di comando dalla parte controllo, che determinano i comportamenti dei registri operativi
  • La parte controllo riceve variabili di condizionamento dalla parte operativa, che determinano i salti a due vie della parte controllo

Vedremo come seguire l'algoritmo passo passo per ottenere questa sintesi a partire dalla descrizione scritta prima.

Da una parte, ciò che si valuta all'esame è solo quanto viene prodotto, mentre il processo seguito per scrivere codice è libera scelta dello studente. Dall'altra, visto che il tempo è necessariamente limitato, avere un processo efficiente permette di esprimere meglio le proprie competenze in tale tempo.

Per questo, vedremo un processo efficiente per fare la sintesi sfruttando l'editor VS Code. Questo sfrutta le scorciatoie dell'editor e l'editing multicaret. Inoltre, avremo vari chekpoint, indicati con 🚩, dove il codice intermedio è compilabile e simulabile, permettendo di controllare di avere ancora lo stesso comportamento della descrizione.

Passo 0: ricopiare su un nuovo file​

Ricopiamo il nostro file di descrizione, sia descrizione.v, su un nuovo file per la sintesi, sia sintesi.v. Nel resto delle istruzioni, assumeremo quindi la descrizione "congelata" e modificheremo il file sintesi.v.

Passo 1: rendere la descrizione omogenea​

Questo processo sfrutta pattern nel codice per eseguire tutte le manipolazioni della descrizione in modo efficiente. Il primo è quindi regolarizzare la descrizione secondo tali pattern.

Per questo, puntiamo a un blocco always @(posedge clock) dove:

  • Ogni stato contiene esplicitamente il comportamento di ciascun registro, anche se questo è conservare.
  • L'assegnamento di ciascun registro è su una riga diversa.
  • Le righe corrispondenti ai vari registri appaiono nello stesso ordine in tutti gli stati.
  • Tutti gli stati e assegmenti seguono la stessa spaziatura: o tutti REG<= o tutti REG <=; o tutti SX: begin↲ o tutti SX:↲begin; end su una riga a sé.

Per il terzo punto, qualunque ordine va bene, purché sia coerente. Otteniamo quindi il seguente codice 🚩.

    always @(posedge clock) if(reset_ == 1) #3 begin
        casex (STAR)
            S0: begin
                SOC <= 1;
                DAV_ <= DAV_;
                MIN <= MIN;
                STAR <= ({eoc1, eoc2, eoc3} == 3'b000) ? S1 : S0;
            end
            S1: begin
                SOC <= 0;
                DAV_ <= DAV_;
                MIN <= out_rc;
                STAR <= ({eoc1, eoc2, eoc3} == 3'b111) ? S2 : S1;
            end
            S2: begin
                SOC <= SOC;
                DAV_ <= 0;
                MIN <= MIN;
                STAR <= (rfd == 1) ? S2 : S3;
            end
            S3: begin
                SOC <= SOC;
                DAV_ <= 1;
                MIN <= MIN;
                STAR <= (rfd == 0) ? S3 : S0;
            end
        endcase
    end
Corrispondenza tra sintesi e descrizione

Se il comportamento di un registro in un dato stato è assente nella descrizione, questo è implicitamente conservazione, e così deve apparire nella sintesi.

Quando si vuole utilizzare un comportamento esplicito per ottimizzazioni, questo va fatto a partire dalla descrizione.

Passo 2: separazione dei blocchi operativi​

Separiamo ora i blocchi operativi dei registri - incluso STAR. Per farlo, cominciamo con ricopiare il blocco always @(posedge clock) tante volte quanti sono i registri. Ciascuna di queste copie verrà poi modificata per lasciare solo gli assegnamenti di uno specifico registro, usando l'editing multicaret.

Vediamo per esempio come ottenere il blocco operativo del registro SOC. Selezioniamo la prima occorrenza di SOC <=, e premiamo ctrl + d tre volte per selezionare tutti gli statement di assegnamento a SOC <=. Queste sono ciascuna la prima riga del proprio stato, e vogliamo che diventino l'unica riga del proprio stato. Possiamo farlo cancellando le 4 righe sotto, usando i tasti home e end per muoversi tra righe di dimensioni diverse. Una volta rimasto un solo assegnemento, possiamo rimuovere anche i begin ... end.

Facciamo quindi lo stesso per tutti i registri, e separiamo anche gli statement di reset. Otteniamo quindi il seguente codice 🚩.

    always @(reset_ == 0) #1 SOC <= 0;
    always @(posedge clock) if(reset_ == 1) #3 begin
        casex (STAR)
            S0: SOC <= 1;
            S1: SOC <= 0;
            S2: SOC <= SOC;
            S3: SOC <= SOC;
        endcase
    end
    
    always @(reset_ == 0) #1 DAV_ <= 1;
    always @(posedge clock) if(reset_ == 1) #3 begin
        casex (STAR)
            S0: DAV_ <= DAV_;
            S1: DAV_ <= DAV_;
            S2: DAV_ <= 0;
            S3: DAV_ <= 1;
        endcase
    end
    
    always @(posedge clock) if(reset_ == 1) #3 begin
        casex (STAR)
            S0: MIN <= MIN;
            S1: MIN <= out_rc;
            S2: MIN <= MIN;
            S3: MIN <= MIN;
        endcase
    end
    
    always @(reset_ == 0) #1 STAR <= 0;
    always @(posedge clock) if(reset_ == 1) #3 begin
        casex (STAR)
            S0: STAR <= ({eoc1, eoc2, eoc3} == 3'b000) ? S1 : S0;
            S1: STAR <= ({eoc1, eoc2, eoc3} == 3'b111) ? S2 : S1;
            S2: STAR <= (rfd == 1) ? S2 : S3;
            S3: STAR <= (rfd == 0) ? S3 : S0;
        endcase
    end

Passo 3: variabili di comando​

In questo passo definiamo per ciascun registro il numero minimo di variabili di comando necessarie per pilotarne il comportamento. Questo numero dipende dal numero di compartomenti distinti di tale registro. Nel caso di SOC e DAV_, abbiamo tre comportamenti: 1, 0 e conservazione. Nel caso di MIN ne abbiamo due: campionamento di out_rc o conservazione.

A livello di codice, dovremmo:

  • sostituire i casex basati su STAR con casex basati sulle variabili di comando
  • aggiungere la definizione delle variabili di comando

Può essere utile fare questo per passaggi successivi, anche se non compilabili, per mantenere il riferimento con la descrizione e riconoscere eventuali errori.

Prendiamo il caso del registro SOC, questo si svolge in tre passi:

  • Si aggiungono delle variabili di comando, senza cancellare gli stati
  • Si aggiunge la definizione di queste variabili, con riferimento agli stati
  • Si cancellano gli stati lasciati prima, ottenendo codice compilabile

Al passo 1, avremo

    always @(reset_ == 0) #1 SOC <= 0;
    always @(posedge clock) if(reset_ == 1) #3 begin
        casex ({b1, b0})
            2'b00 S0: SOC <= 1;
            2'b01 S1: SOC <= 0;
            2'b1X S2: SOC <= SOC;
            2'b1X S3: SOC <= SOC;
        endcase
    end

Al passo 2, scriviamo

    wire b1, b0;
    assign #1 {b1, b0} = 
        (STAR == S0)? 2'b00 :
        (STAR == S1)? 2'b01 :
        (STAR == S2)? 2'b1X :
        (STAR == S3)? 2'b1X :
        /*default*/

Questa notazione a tabella torna molto utile più avanti, quando scriveremo la ROM.

Al passo 3, cancelliamo gli stati dal blocco @(posedge clock) per riottenere codice valido, ed eliminiamo i doppioni.

    always @(reset_ == 0) #1 SOC <= 0;
    always @(posedge clock) if(reset_ == 1) #3 begin
        casex ({b1, b0})
            2'b00: SOC <= 1;
            2'b01: SOC <= 0;
            2'b1X: SOC <= SOC;
        endcase
    end

Il video seguente mostra come questo procedimento può essere applicato a tutti i registri dell'esercizio.

Otteniamo quindi il seguente codice 🚩.

    always @(reset_ == 0) #1 SOC <= 0;
    always @(posedge clock) if(reset_ == 1) #3 begin
        casex ({b1, b0})
            2'b00: SOC <= 1;
            2'b01: SOC <= 0;
            2'b1X: SOC <= SOC;
        endcase
    end

    always @(reset_ == 0) #1 DAV_ <= 1;
    always @(posedge clock) if(reset_ == 1) #3 begin
        casex ({b3, b2})
            2'b00: DAV_ <= DAV_;
            2'b01: DAV_ <= 0;
            2'b1X: DAV_ <= 1;
        endcase
    end

    always @(posedge clock) if(reset_ == 1) #3 begin
        casex (b4)
            1'b0: MIN <= MIN;
            1'b1: MIN <= out_rc;
        endcase
    end

    wire b4, b3, b2, b1, b0;
    assign #1 {b4, b3, b2, b1, b0} =
        (STAR == S0) ? 5'b00000 :
        (STAR == S1) ? 5'b10001 :
        (STAR == S2) ? 5'b0011X :
        (STAR == S3) ? 5'b01X1X :
        /*default*/    5'bXXXXX ;
Ottimizzare la codifica

La procedura mostrata definisce le variabili di comando e le rispettive codifiche indipendentemente. È talvolta possibile ridurre il numero complessivo di variabili di comando trovando codifiche che permettano di usare la stessa variabile per più registri. Questa è una ottimizzazione solo se non si aggiunge alcuna variabile di comando a nessun registro.

Non usare la codifica dello stato

L'obiettivo delle variabili di comando è ottimizzare la dimensione dei multiplexer in input a ciascun registro: usare il registro STAR significa usare un multiplexer a tanti ingressi quanti sono gli stati, mentre un registro operativo ha tipicamente molti meno comportamenti distinti.

Usare direttamente la codifica dello stato è un errore grave, a meno che non si dimostri che sia proprio la codifica più efficiente. A tale scopo, usare commenti nel codice.

Passo 4: variabili di condizionamento​

In questo passo definiamo il numero minimo di variabili necessarie per guidare i cambi di stato della parte controllo. Per far questo, dobbiamo guardare alle condizioni indipendenti dei salti a due vie.

    always @(reset_ == 0) #1 STAR <= 0;
    always @(posedge clock) if(reset_ == 1) #3 begin
        casex (STAR)
            S0: STAR <= ({eoc1, eoc2, eoc3} == 3'b000) ? S1 : S0;
            S1: STAR <= ({eoc1, eoc2, eoc3} == 3'b111) ? S2 : S1;
            S2: STAR <= (rfd == 1) ? S2 : S3;
            S3: STAR <= (rfd == 0) ? S3 : S0;
        endcase
    end

In questo caso notiamo che le condizioni di S2 e S3 sono una la negazione dell'altra: non sono indipendenti. Possiamo guidare entrambi i salti con una sola variabile di condizionamento, se invertiamo uno dei due salti. In questo caso, scegliamo di invertire il salto in S3.

Otteniamo quindi il seguente codice 🚩.

    wire c2, c1, c0;
    assign #1 c0 = {eoc1, eoc2, eoc3} == 3'b000;
    assign #1 c1 = {eoc1, eoc2, eoc3} == 3'b111;
    assign #1 c2 = rfd == 1;

    always @(reset_ == 0) #1 STAR <= 0;
    always @(posedge clock) if(reset_ == 1) #3 begin
        casex (STAR)
            S0: STAR <= c0 ? S1 : S0;
            S1: STAR <= c1 ? S2 : S1;
            S2: STAR <= c2 ? S2 : S3;
            S3: STAR <= c2 ? S0 : S3;
        endcase
    end

Le variabili di condizionamento vanno sintetizzate a livello di bit, sostituendo ai confronti con == le corrispondenti espressioni con porte logiche. In questo caso, otteniamo 🚩

    assign #1 c0 = ~eoc1 & ~eoc2 & ~eoc3;
    assign #1 c1 = eoc1 & eoc2 & eoc3;
    assign #1 c2 = rfd;
Quando invertire i salti

Viene considerata valida anche una sintesi che usi il numero minimo di variabili di condizionamento ma senza invertire i salti nel Verilog. Per esempio, si può scrivere S3: STAR <= ~c2 ? S3 : S0;. Tuttavia non si ha questa libertà nella ROM, dove l'inversione è obbligatoria. Dato che la ROM si fa di solito in fondo è facile dimenticarsene, ed è quindi consigliato di invertire già nel Verilog della parte controllo.

Sintesi a livello di bit

La richiesta di sintesi delle variabili di condizionamento è flessibile per esercizi dove si hanno molti bit (per esempio, un registro COUNT a 16 bit ). Nel dubbio, si può chiedere durante l'esame.

Passo 5: separare le parti​

Fin a questo punto abbiamo modificato il codice della rete senza separare effettivamente la parte operativa dalla parte controllo. Questo è utile per mantenere la rete simulabile e controllare di non aver introdotto nuovi errori rispetto alla descrizione.

Arrivati a questo punto possiamo separare le parti. Nella parte operativa andranno i registri operativi, le reti combinatorie che ne pilotano gli ingressi, e le reti combinatorie che generano le variabili di condizionamento. A questa parte vengono inoltre collegati gli ingressi e le uscite della rete complessiva. Nella parte controllo, invece, ci sarà solo il registro STAR e la ROM a microindirizzi, di cui scriviamo in Verilog, in particolare, la parte che genera le variabili di controllo.

Otteniamo quindi il seguente codice 🚩.

module ABC(
    x1, x2, x3,
    eoc1, eoc2, eoc3,
    soc,
    min, dav_, rfd,
    clock, reset_
);
    input [7:0] x1, x2, x3;
    input eoc1, eoc2, eoc3;
    output soc;
    output [7:0] min;
    output dav_;
    input rfd;
    input clock, reset_;

    wire b4, b3, b2, b1, b0;
    wire c2, c1, c0;

    ABC_PO po(
        x1, x2, x3,
        eoc1, eoc2, eoc3,
        soc,
        min, dav_, rfd,
        b4, b3, b2, b1, b0,
        c2, c1, c0
        clock, reset_,
    );

    ABC_PC pc(
        b4, b3, b2, b1, b0,
        c2, c1, c0
        clock, reset_,
    );
endmodule

module ABC_PO(
    x1, x2, x3,
    eoc1, eoc2, eoc3,
    soc,
    min, dav_, rfd,
    b4, b3, b2, b1, b0,
    c2, c1, c0
    clock, reset_,
);
    input [7:0] x1, x2, x3;
    input eoc1, eoc2, eoc3;
    output soc;
    output [7:0] min;
    output dav_;
    input rfd;
    input clock, reset_;

    reg SOC;
    assign soc = SOC;
    reg [7:0] MIN;
    assign min = MIN;
    reg DAV_;
    assign dav_ = DAV_;

    wire [7:0] out_rc;
    MINIMO_3 min_rc(
        .a(x1), .b(x2), .c(x3),
        .min(out_rc)
    );

    input b4, b3, b2, b1, b0;
    output c2, c1, c0;

    assign #1 c0 = ~eoc1 & ~eoc2 & ~eoc3;
    assign #1 c1 = eoc1 & eoc2 & eoc3;
    assign #1 c2 = rfd;

    always @(reset_ == 0) #1 SOC <= 0;
    always @(posedge clock) if(reset_ == 1) #3 begin
        casex ({b1, b0})
            2'b00: SOC <= 1;
            2'b01: SOC <= 0;
            2'b1X: SOC <= SOC;
        endcase
    end

    always @(reset_ == 0) #1 DAV_ <= 1;
    always @(posedge clock) if(reset_ == 1) #3 begin
        casex ({b3, b2})
            2'b00: DAV_ <= DAV_;
            2'b01: DAV_ <= 0;
            2'b1X: DAV_ <= 1;
        endcase
    end

    always @(posedge clock) if(reset_ == 1) #3 begin
        casex (b4)
            1'b0: MIN <= MIN;
            1'b1: MIN <= out_rc;
        endcase
    end
endmodule

module ABC_PC(
    b4, b3, b2, b1, b0,
    c2, c1, c0
    clock, reset_,
);
    input clock, reset_;

    output b4, b3, b2, b1, b0;
    input c2, c1, c0;

    reg [1:0] STAR;
    localparam 
        S0 = 0,
        S1 = 1,
        S2 = 2,
        S3 = 3;

    assign #1 {b4, b3, b2, b1, b0} =
        (STAR == S0) ? 5'b00000 :
        (STAR == S1) ? 5'b10001 :
        (STAR == S2) ? 5'b0011X :
        (STAR == S3) ? 5'b01X1X :
        /*default*/    5'bXXXXX ;

    always @(reset_ == 0) #1 STAR <= 0;
    always @(posedge clock) if(reset_ == 1) #3 begin
        casex (STAR)
            S0: STAR <= c0 ? S1 : S0;
            S1: STAR <= c1 ? S2 : S1;
            S2: STAR <= c2 ? S2 : S3;
            S3: STAR <= c2 ? S0 : S3;
        endcase
    end
endmodule

// sintesi di rete combinatoria omessa

Passo 6: la ROM​

Secondo il modello a microindirizzi, la parte controllo è implementata come una ROM che usa il registro STAR come microindirizzo, e fornisce in uscita le variabili di controllo per la parte operativa così come c_eff, m_true e m_false. Questi ultimi tre elementi, insieme alle variabili di condizionamento in ingresso dalla parte operativa, sono utilizzati con dei multiplexer in cascata per determinare lo stato successivo della rete. Lo schema circuitale è il seguente.

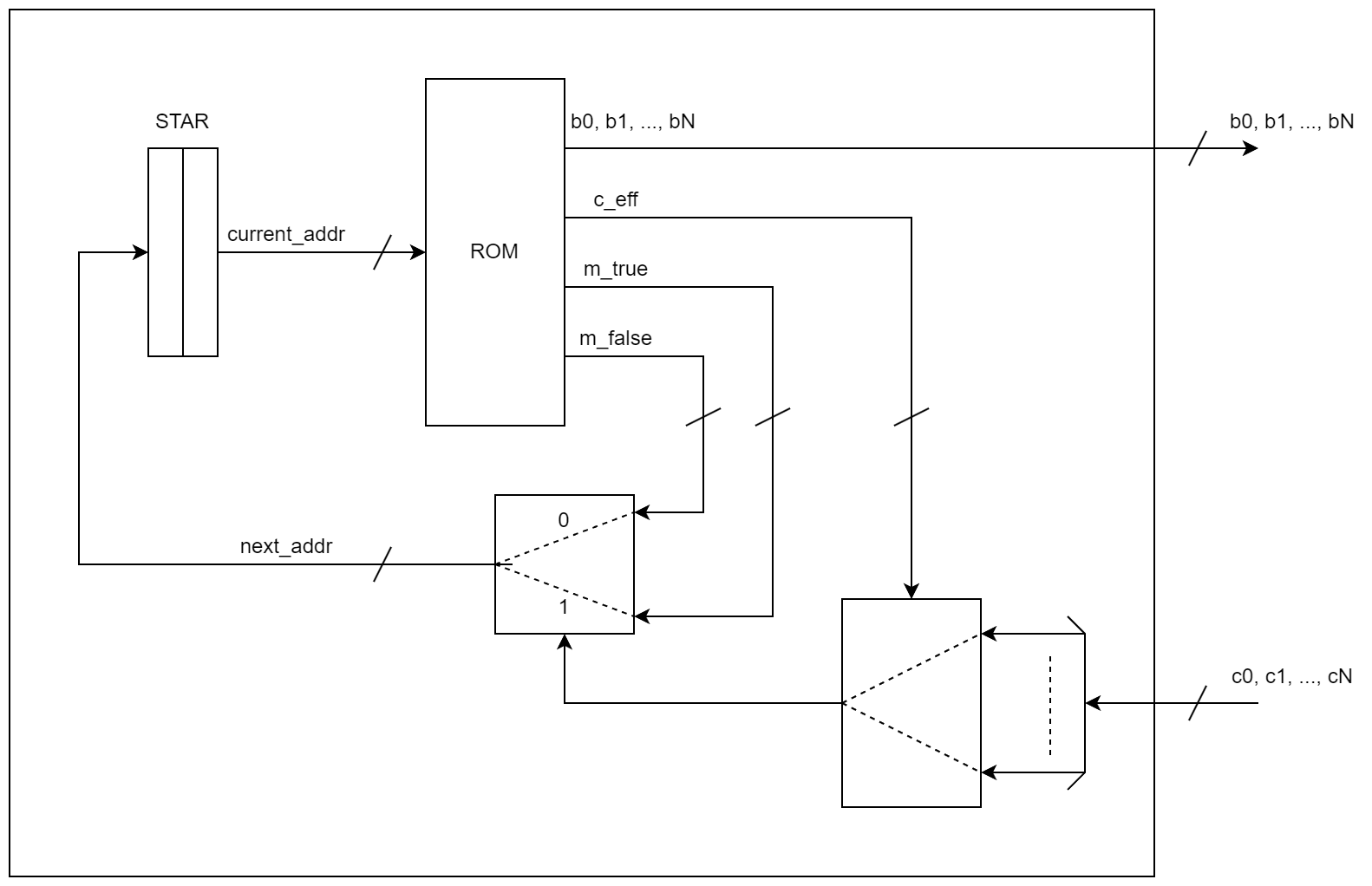
Fare la sintesi direttamente come ROM è possibile, ma è ben più tedioso e difficile da debuggare. Per questo manteniamo il linguaggio di trasferimento tra registri per indicare in Verilog il comportamento di STAR, e scriviamo invece come commento nel codice una tabella che mostri il contenuto della ROM.

Per evitare ogni ambiguità, si comincia specificando codifiche binarie per gli stati e i nomi delle variabili di comando. Dopodiché, si può riempire la tabella con quanto scritto in Verilog.

/*
    S0 = 00, S1 = 01, S2 = 10, S3 = 11
    c0 = 00, c1 = 01, c2 = 1X

    M-addr |  b4, b3, b2, b1, b0 | c_eff | M-addr-T | M-addr-F
    ----------------------------------------------------------
    00     | 00000               | 00    | 01       | 00
    01     | 01100               | 01    | 10       | 01      
    10     | 1X001               | 1X    | 10       | 11
    11     | 1X01X               | 1X    | 00       | 11
*/

A questo punto la sintesi è completa. È scaricabile qui.

Menzioniamo a parte il caso dei salti incondizionati, del tipo del tipo STAR <= S1. In questo caso, va scritta la ROM in modo che next_address sia S1 per qualunque valore delle variabili di condizionamento. Questo si può ottenere mettendo sia m_true che m_false a S1, lasciando non-specificato c_eff. In tabella, questo si traduce in

/*
    ... | c_eff | M-addr-T | M-addr-F
    ----------------------------------
    ... | X     | 01       | 01
*/
Formattazione della tabella

Non essendo parte del codice, non c'è una sintassi o formattazione precisa da seguire per la tabella, purché sia non-ambigua quando letta dai docenti. Questo include le varie alternative come m-true, m-addr-true, m-T etc., o usare ? al posto di X.

Valori non specificati

La tabella della ROM è difatto una tabella di verità per una rete combinatoria, che è quindi sintetizzabile utilizzando i metodi visti come le mappe di Karnaugh.

I valori non specificati per variabili di comando e condizionamento sono quindi utili per permettere ottimizzazioni in tale sintesi.

Salti incodinzionati, non indeterminati

È purtroppo frequente vedere ROM dove uno o entrambi gli indirizzi m_true o m_false sono non specificati, come nell'esempio seguente

/*
    ... | c_eff | M-addr-T | M-addr-F
    ----------------------------------
    ... | X     | 01       | X          Errore!
*/

Una ROM del genere è priva di senso, perché determina una rete che salta a uno stato a caso.